Table of Contents

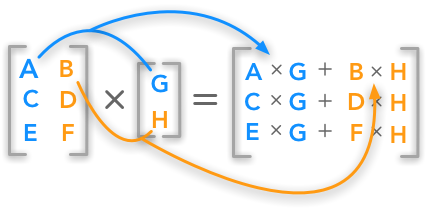
Unveiling the Power of the Matrix Product: A Comprehensive Guide

In the realm of linear algebra, the matrix product stands as a fundamental operation, underpinning a vast array of applications across diverse fields. From computer graphics and data analysis to physics and engineering, the ability to efficiently and accurately compute the matrix product is crucial. This article delves into the intricacies of the matrix product, exploring its definition, properties, applications, and computational considerations. We aim to provide a comprehensive understanding of this essential mathematical tool, suitable for both beginners and those seeking a deeper insight.

What is the Matrix Product?

The matrix product, also known as matrix multiplication, is a binary operation that produces a matrix from two matrices. For the matrix product of two matrices A and B to be defined, the number of columns in A must equal the number of rows in B. If A is an m × n matrix and B is an n × p matrix, then their matrix product C is an m × p matrix. The element c_ij in the resulting matrix C is calculated as the dot product of the i-th row of A and the j-th column of B.

Mathematically, this can be expressed as:

c_ij = ∑_k=1ⁿ a_ik * b_kj

Where:

c_ij is the element in the i-th row and j-th column of the resulting matrix C.
a_ik is the element in the i-th row and k-th column of matrix A.
b_kj is the element in the k-th row and j-th column of matrix B.
n is the number of columns in matrix A and the number of rows in matrix B.

It’s important to remember that the order of matrices matters. In general, A * B ≠ B * A. This property, known as non-commutativity, is a key characteristic of the matrix product and distinguishes it from scalar multiplication.

Properties of the Matrix Product

The matrix product possesses several important properties that are fundamental to its application and understanding:

Associativity: (A * B) * C = A * (B * C). This property allows us to group matrices in different ways when performing multiple multiplications.
Distributivity: A * (B + C) = A * B + A * C and (A + B) * C = A * C + B * C. The matrix product distributes over matrix addition.
Identity Matrix: The identity matrix, denoted by I, is a square matrix with ones on the main diagonal and zeros elsewhere. For any matrix A, A * I = A and I * A = A.
Transpose: (A * B)^T = B^T * A^T. The transpose of a matrix product is the product of the transposes in reverse order.
Scalar Multiplication: (k * A) * B = A * (k * B) = k * (A * B), where k is a scalar.

Applications of the Matrix Product

The matrix product is a cornerstone of many computational and mathematical applications. Its ability to represent and manipulate linear transformations makes it invaluable in a wide range of fields:

Computer Graphics

In computer graphics, transformations such as scaling, rotation, and translation are represented by matrices. The matrix product is used to combine these transformations into a single matrix, allowing for efficient application of complex transformations to 3D models. Each vertex of a model can be represented as a vector, and by multiplying this vector by the transformation matrix, the new position of the vertex can be determined. This is crucial for rendering realistic and dynamic scenes.

Data Analysis and Machine Learning

The matrix product is extensively used in data analysis and machine learning. It forms the basis of many algorithms, including linear regression, principal component analysis (PCA), and neural networks. In neural networks, the weighted sum of inputs to a neuron is calculated using the matrix product. The weights are stored in a matrix, and the inputs are represented as a vector. The matrix product efficiently computes the output of each layer in the network.

Linear Systems of Equations

Systems of linear equations can be represented in matrix form as A * x = b, where A is a matrix of coefficients, x is a vector of unknowns, and b is a vector of constants. Solving for x often involves finding the inverse of matrix A. The matrix product is used to verify the solution by checking if A * x indeed equals b. Techniques like Gaussian elimination and LU decomposition heavily rely on matrix product operations.

Physics and Engineering

In physics, the matrix product is used to represent linear transformations in quantum mechanics, such as rotations and Lorentz transformations. It is also used in structural analysis to calculate the forces and stresses in structures. In electrical engineering, the matrix product is used to analyze circuits and solve for currents and voltages.

Cryptography

Certain cryptographic algorithms leverage the properties of the matrix product for encryption and decryption. The complexity of inverting large matrices can be used to create secure cryptographic systems. The matrix product itself is not typically used directly as an encryption algorithm, but it forms the basis for more complex schemes.

Computational Considerations

While the matrix product is a fundamental operation, its computational complexity can be significant, especially for large matrices. The standard algorithm for multiplying an m × n matrix by an n × p matrix has a time complexity of O(m*n*p). This means that the number of operations required grows cubically with the size of the matrices.

For large matrices, more efficient algorithms have been developed, such as Strassen’s algorithm and Coppersmith–Winograd algorithm. These algorithms have lower asymptotic time complexities, but they may have higher overhead costs, making them practical only for very large matrices. Optimizing the matrix product is an active area of research, with ongoing efforts to develop even faster and more efficient algorithms.

Furthermore, libraries like BLAS (Basic Linear Algebra Subprograms) and LAPACK (Linear Algebra PACKage) provide highly optimized implementations of the matrix product and other linear algebra operations. These libraries are often used in scientific computing and data analysis to achieve high performance.

Examples of Matrix Product Calculations

Let’s consider two simple matrices to illustrate the calculation of the matrix product:

A = [[1, 2], [3, 4]]

B = [[5, 6], [7, 8]]

To calculate the matrix product C = A * B, we perform the following calculations:

c₁₁ = (1 * 5) + (2 * 7) = 5 + 14 = 19

c₁₂ = (1 * 6) + (2 * 8) = 6 + 16 = 22

c₂₁ = (3 * 5) + (4 * 7) = 15 + 28 = 43

c₂₂ = (3 * 6) + (4 * 8) = 18 + 32 = 50

Therefore, C = [[19, 22], [43, 50]]

This simple example demonstrates the process of calculating the matrix product. For larger matrices, the calculations become more complex, but the underlying principle remains the same.

Conclusion

The matrix product is a fundamental operation in linear algebra with widespread applications across various fields. Its ability to represent and manipulate linear transformations makes it an indispensable tool for solving complex problems in computer graphics, data analysis, physics, engineering, and more. Understanding the properties and computational aspects of the matrix product is crucial for anyone working with linear algebra and its applications. As computational power continues to increase, the matrix product will undoubtedly remain a cornerstone of scientific computing and data-driven innovation. [See also: Linear Algebra Fundamentals] [See also: Matrix Inversion Techniques] [See also: Applications of Linear Transformations]